Glossar
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
A |
|---|
| SK | abhängige Variable | ||
|---|---|---|---|
Variable, die durch andere (unabhängige) Variablen (UV) erklärt oder vorhergesagt werden soll. | |||
| SK | ALM | ||
|---|---|---|---|
Das allgemeine lineare Modell (ALM, englisch: general linear model) ist ein Überbegriff für viele verschiedene statistische Tests. Es wird bei der Vorhersage eines kontinuierlichen/ metrischen Kriteriums (z.B. die erreichte Punktanzahl in einem Test) durch metrische und/oder kategoriale Prädiktoren genutzt. Es gibt verschiedene Spezialfälle des ALMs, die sich je in Skalenniveau und Anzahl der Prädiktoren unterscheiden. Wenn nur eine bzw. mehrere metrische Prädiktoren zur Vorhersage genutzt werden, handelt es sich um eine einfache bzw. multiple lineare Regression, bei rein kategorialen Prädiktoren um eine kategoriale Regression, ANOVA oder einen t-Test und bei einer Kombination aus beiden um eine Kovarianzanalyse. Ein Beispiel wäre die Frage, welche Punktzahl zu erreichen ist (AV, metrisches Kriterium), wenn eine Person eine bestimmte Anzahl an Stunden gelernt hat (UV, metrischer Prädiktor) und Nachhilfe nimmt oder nicht (UV, dichotom Prädiktor). | |||
B |
|---|
| SK | Bootstrapping | ||
|---|---|---|---|
Unter Bootstrapping versteht man eine Resampling Methode, bei der eine empirische Verteilung (zum Beispiel die Stichprobenkennwerteverteilung) durch die erneute zufällige Stichprobenziehung aus dem Ursprungsdatensatz aufgestellt wird. Das heißt, es werden i.d.R. mehrfach immer gleich große Stichproben "mit zurücklegen" aus dem Ursprungsdatensatz gezogen. Dabei geht man davon aus, dass der vorliegende Ursprungsdatensatz und die darauf gezogene Zufallsstichproben repräsentativ für die Grundgesamtheit ist. Die Methode ist besonders dafür geeignet, um Standardfehler und Konfidenzintervalle aus der durch Bootstrap erlangten Stichprobenkennwerteverteilung zu berechnen, wenn die Verteilung sonst nicht oder nur kompliziert herzuleiten wäre (z.B. für den indirekten Effekt in der Mediation). Hier findest du noch eine anschauliche Beschreibung Efron, B. (1979). Bootstrap Methods: Another Look at the Jackknife. The Annals of Statistics, 7(1), 1–26. doi:10.1214/aos/1176344552 | |||
G |
|---|
| SK | GLM | ||
|---|---|---|---|
Das generalisierte lineare Modell (GLM, englisch: generalized linear model) ist eine Verallgemeinerung
des ALM. Es wird genutzt, um abhängige Variablen mit nicht
normalverteilten Residuen(sondern z.B. binomial- oder
poissonverteilten Residuen) modellieren. Das geschieht über eine
sogenannte Linkfunktion. Ein häufiger anderer Spezialfall ist die logistische Regression für die Vorhersage eines dichotomen Kriteriums(z.B. Aufgabe gelöst: Ja oder nein) durch metrische und/oder kategoriale Prädiktoren. Dabei modelliert die logistische Regression die vorhergesagte Wahrscheinlichkeit für eine Ausprägung des Kriteriums. Die Prädiktoren können zu einer Zunahme der vorhergesagten Wahrscheinlichkeit (positiver Zusammenhang) oder für eine Abnahme der vorhergesagten Wahrscheinlichkeit (negativer Zusammenhang) führen. Ein Beispiel wäre die Frage, mit welcher Wahrscheinlichkeit eine Aufgabe gelöst wird (abhängige Variable/dichotomes Kriterium - binomialverteilt) abhängig davon, wie viele Stunden eine Person gelernt hat (unabhängige Variable, metrischer Prädiktor) und Nachhilfe nimmt oder nicht (unabhängige Variable, dichotomer Prädiktor). | |||
I |
|---|
| SK | Intervallskaliert | ||
|---|---|---|---|
Die Intervallskala gehört zu den metrischen Skalen. Das bedeutet, dass die Werte einer Intervallskala in einer Intervallskala in eine sinnvolle Reihenfolge gebracht werden können und dabei auch der Abstand zwischen den Zahlen interpretiert werden darf. Dabei besitzt die Intervallskala allerdings keinen sinnvoll zu interpretierenden Nullpunkt. Ein Beispiel für eine intervallskalierte Variable ist die Temperatur: es gibt zwar einen "Nullpunkt" mit 0 Grad Celsius, dieser ist allerdings nicht natürlich, sondern wurde willkürlich festgelegt. Die unterschiedlichen Skalenniveaus können in eine Reihenfolge gebracht werden, bei der von links nach rechts das Informationsniveau steigt: Nominalskala | Ordinalskala | Intervallskala | Verhältnisskala | |||
K |
|---|
| SK | kategorial | |
|---|---|---|
Kategoriale Variablen haben eine endliche Anzahl an Kategorien als Ausprägungen. Wenn dabei die unterschiedlichen Kategorien nicht in eine sinnvolle Reihenfolge gebracht werden können, spricht man von nominalskalierten Variablen. Können die unterschiedlichen Kategorien in eine sinnvolle Reihenfolge gebracht werden, spricht man von ordinalskalierten Variablen. gruppiert, nominalskaliert, ordinalskaliert? | ||
| SK | Konfidenzintervall | ||
|---|---|---|---|
Das Konfidenzintervall (KI, typischerweise 95%-KI) ist eine Verrechnung des Standardfehlers und damit ein Maß für die Unsicherheit in der Schätzung eines Parameters. Wenn man die selbe Analyse an einer gleich großen Stichprobe aus der selben Population unendlich oft wiederholen würde, dann würde das KI in 95% der Fälle den tatsächlichen Parameterwert der Population beinhalten. | |||
| SK | Konfidenzintervalle Interpretationshilfe | |
|---|---|---|
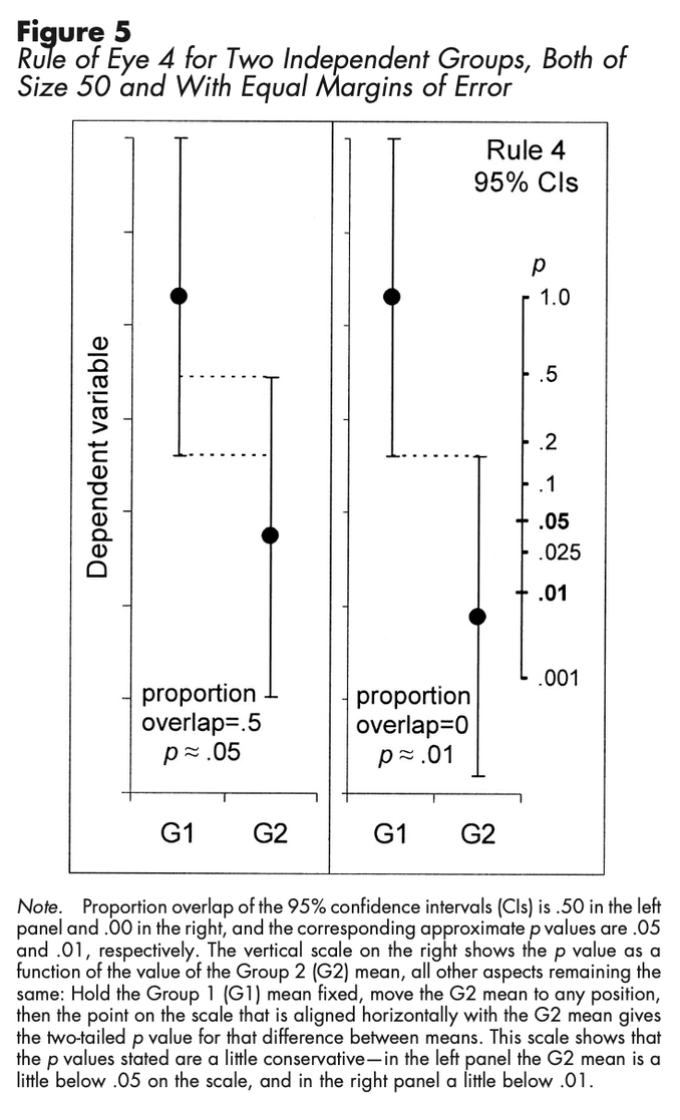
Der Einsatz von Intervallschätzern in der psychologischen Forschung hat das Potenzial die Kommunikation von Ergebnissen zu verbessern. Konfidenzintervalle haben unter anderem den Vorteil, dass sie in Relation zu p-Werten aus der klassischen inferenzstatistischen Nullhypothesen-Signifikanztestung (NHST) stehen und gleichzeitig dabei helfen können, über dichotome Entscheidungen beim NHST (p < .05 vs. p > .05) hinauszugehen. Dafür sind Konfidenzintervalle gerade in Grafiken nützlich, insbesondere wenn direkt die interessierenden Punktschätzer und deren Konfidenzintervalle dargestellt werden (beispielsweise bei einem t-Test direkt die geschätzte Differenz zwischen zwei Gruppen und das Konfidenzintervall der Differenz). Dazu sollte Klarheit darüber geschaffen werden, wie die Grafik zu verstehen ist, d.h. ob Konfidenzintervalle, Standardfehler oder Standardabweichungen als Fehlerbalken dargestellt sind und auf Basis welchen Forschungsdesigns die Ergebnisse entstanden sind (bspw. ob es Messwiederholung gab). Ist das gegeben, können Daumenregeln zur (visuellen) Interpretation von Ergebnisgrafiken anhand von Konfidenzintervallen angewendet werden: u.a. (1) Das Konfidenzintervall kann so verstanden werden, dass Werte innerhalb des Intervalls plausibel erscheinen und Werte außerhalb des Intervalls eher nicht (dabei sollte aber nicht zu viel Gewicht darauf gelegt werden, ob ein interessierender Wert gerade nicht oder gerade schon im Konfidenzintervall enthalten ist, um Entscheidungen nicht zu stark zu Dichotomisieren), (2) die Fehlermarge (Hälfte der Länge des gesamten Konfidenzintervalls) kann als Indikator für die Präzision der Studie verstanden werden (größere Fehlermarge, ungenauere Schätzung), (3) im Fall von unabhängigen Stichproben ist p < .05 wenn sich die 95%-Konfidenzintervalle der beiden Mittelwerte nicht mehr als die Hälfte der durchschnittlichen Fehlermarge überschneiden (siehe Abbildung; das gilt nur sofern die Stichprobengröße in jeder Gruppe mindestens 10 ist und die beiden Fehlermargen sich nicht mehr als um den Faktor 2 unterscheiden), (4) dies ist nicht auf abhängige Stichproben übertragbar, hier sollte man sich auf den Mittelwert der Differenzen und dessen Konfidenzintervall konzentrieren (interessant ist hier, inwiefern die 0 im Konfidenzintervall eingeschlossen ist), (5) auch im Kontext von Konfidenzintervallen ist es notwendig über die praktische Relevanz und Größe eines etwaigen Effekts nachzudenken anstatt sich nur auf die statistisch Signifikanz/Bedeutung zu fokussieren (beispielsweise bei einem unabhängigen t-test ist also nicht nur die Überlappung der Konfidenzintervalle zu achten, sondern auch, inwiefern der Unterschied zwischen den beiden Gruppen überhaupt auch eine praktische Relevanz hat). Interpretationshilfen gibt es auch für Standardfehler als Fehlerbalken, wobei Konfidenzintervalle im Kontext von Ergebnisgrafiken Vorteile gegenüber Standardfehler-Balken mit sich bringen. Übergreifend besteht das Problem, dass es nicht in allen Fällen einfach möglich ist, überhaupt ein Konfidenzintervall zu berechnen und die grafische Ergebnisdarstellung bei komplexeren Studiendesigns schnell schwierig und unübersichtlich wird.
Quelle/Noch mehr zu Konfidenzintervallen: Cumming, G. & Finch, S. (2005b). Inference by Eye: Confidence Intervals and How to Read Pictures of Data. American Psychologist, 60(2), 170–180. https://doi.org/10.1037/0003-066x.60.2.170 | ||
| SK | Kontraste | ||
|---|---|---|---|
Kontraste werden beim Testen von Hypothesen über die Mittelwertsunterschiede in einer ANOVA gebildet. Die Summe aller Kontraste muss immer 0 sein. unabhängige Kontraste testen von einander unabhängige Hypothesen über die Mittelwertsunterschiede in einer ANOVA. Dabei kommt es darauf an, dass die Hypothesen sich nicht auf den selben Mittelwert in Abhängigkeit anderer Mittelwerte bezieht. z.B. K11= - 2, K12= 1, K13= 1 Hypothese: μ1= (μ2+ μ3)/2 K21= 0, K22= -1, K23= 1 Hypothese: μ2= μ3 Das sind unabhängige Kontraste weil einmal der Unterschied von μ1 zu den anderen Mittelwerten untersucht wird und der zweite Kontrast μ1 nicht mit einbezieht, es also keine Interaktion zwischen den Hypothesen geben kann. | |||
L |
|---|
| SK | latent | ||
|---|---|---|---|
Als latent werden Variablen bezeichnet die sich nicht direkt aus Beobachtung erschließen bzw. messen lassen. Zu diesen Variablen zählen z.B. Einstellungen, Persönlichkeit oder aber auch Motivation oder Depressionen. Um einen Rückschluss auf diese Variablen zu ziehen müssen messbare Variablen, z.B. Items eines Fragebogens, oder Verhalten, z.B. wie wie häufig schafft es eine Person mit Depressionen morgen nicht aus dem Bett, herangezogen werden um auf die latente Variable zu schließen (Messmodell). | |||