Suppression
Was ist Suppression?
Suppression ist ein statistisches Phänomen, wobei der am häufigsten auftretende Fall ist, dass ein Effekt unerwarteterweise größer wird, wenn der Effekt um eine dritte Variable bereinigt wird. Suppression kann in verschiedenen Analysen auftreten (Korrelationsanalysen, Mediationsanalysen, Multiple Regression, SEM, …).
-
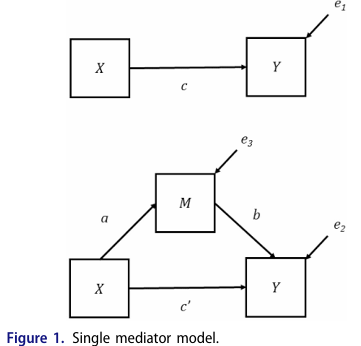
Beispiel: X und M als Prädiktoren eines Kriteriums Y. Wenn M und Y unabhängig voneinander sind oder nur sehr schwach zusammenhängen, kann M die Vorhersagekraft von X erhöhen, indem M Kriterium-irrelevantes Rauschen in X unterdrückt. So verbessert sich die Vorhersage von Y durch X. Das Modell Y ~ X + M ist also besser als Y ~ X , obwohl Y unabhängig von M ist (oder nur gering damit zusammenhängt)
Es gibt unterschiedliche Arten von Suppression: Neben einem unerwarteten Anstieg des Effekts kann es beispielsweise auch zu einem Vorzeichenwechsel des Effekts kommen („negative Suppression“). Wir konzentrieren uns hier nur auf den Fall Anstieg im Effekt.
Wie kann man feststellen, ob Suppression vorliegt?
Wir stellen hier 3 mögliche deskriptive Kriterien dafür, ob Suppression vorliegt, vor (siehe Tabelle). Das a*b*c’ Kriterium ist inferenzstatistisch am besten geeignet (siehe nächster Abschnitt; Muniz & MacKinnon, 2025). Zwei der Kriterien arbeiten mit Korrelation vs. Partialkorrelation, eins mit direkten vs. indirekten Effekten einer Regression bzw. eines SEMs (Korrelationen und Regressionsgewichte lassen sich ineinander überführen).
|
Velicer Kriterium |
Sharpe & Roberts Kriterium |
a*b*c’ Kriterium |
|
\( r^2_{my} - r^2_{my.x} < 0 \) \( = r^2_{my} < \frac{(r_{my}- r_{xy} \cdot r_{xm})^2}{1 - r^2_{xm}} \)
|
\( r_{xm} - \frac{2\gamma}{1 + \gamma^2} > 0 \) mit \( \gamma = \frac{r_{xy}}{r_{my}} \) wenn \( r_{xm} > 0 \) oder \( r_{xm} - \frac{2\gamma}{1 + \gamma^2} < 0 \) wenn \( r_{xm} < 0 \) |
\( a \cdot b \cdot c' < 0 \)
|
|
Velicer, W. F. (1978). Suppressor Variables and the Semipartial Correlation Coefficient. Educational and Psychological Measurement, 38(4), 953-958. https://doi.org/10.1177/001316447803800415
|
Sharpe, N. R., & Roberts, R. A. (1997). The Relationship among Sums of Squares, Correlation Coefficients, and Suppression. The American Statistician, 51(1), 46–48. https://doi.org/10.1080/00031305.1997.10473587
|
MacKinnon, D. P., Krull, J. L. & Lockwood, C.M. (2000). Equivalence of the mediation, confounding and suppression effect. Prevention Science: The Official Journal of the Society for Prevention Research, 1(4), 173–181. |
-
Diese Kriterien gelten nur für Modelle mit 3 metrischen Variablen mit linearen Zusammenhängen!
-
Sie können nicht ermitteln welche der Variablen X oder M als Suppressor fungiert (das ist eine inhaltliche Frage, man kommt zu den gleichen Schätzungen wenn M oder X als Suppressor betrachtet wird)
Wie kann man bei Vorliegen von Suppression herausfinden, ob sie statistisch signifikant ist?
Von den Kriterien aus der Tabelle ist a*b*c‘ als Teststatistik am besten geeignet. Formeln für die Signifikanzprüfung (dabei steht SE für standard error, also dem Standardfehler des jeweiligen Parameters):

-
Der Critical Value Test ist ein empirischer Z-Wert, es gilt also Z-empirisch > 1.96 als signifikant
-
Die Autoren empfehlen zusätzlich die Berechnung von Bootstrap-Konfidenzintervallen zur Intervallschätzung – der Test ist dann signifikant, wenn der Wert Null nicht im Bootstrap Konfidenzintervall enthalten ist.
Limitationen des a*b*c‘ Tests
Der Ansatz a*b*c‘ kann Suppression nicht detektieren bei vollständiger Mediation (c‘ = 0)! Denn wenn c‘ = 0 dann a*b*c‘ = 0 (also keine Suppression nach dem Kriterium < 0). In diesem Fall der vollständigen Mediation lohnt sich eine Entscheidung nach dem Velicer Kriterium (deskriptiv). Außerdem wurde der Signifikanztest unter Annahme einer Normalverteilung des Schätzers entwickelt, diese Annahme kann falsch sein, daher kann man robuste Bootstrap Konfidenzintervalle verwenden (auch Bayes-Kredibilitätsintervalle sind denkbar).
Muniz, F. B. & MacKinnon, D. P. (2025). Three Approaches to Testing for Statistical Suppression. Multivariate Behavioral Research, 68(2). DOI: 10.1080/00273171.2025.2483245